- Tủ lạnh giảm sốc đến 50% Khuyến mãi mới
- SALE KHỔNG LỒ - GIẢM SỐC 21 - 50%
- Tháng Panasonic - quà ngập nhà
- Đổi tủ lạnh - Máy lạnh cũ lấy PANASONIC thu hồi 2 triệu
- Đổi máy giặt cũ lấy PANASOIC thu hồi 2 triệu
- Tháng 9 may mắn cũng Panasonic
- Nội thất sale khổng lồ
![Khuyến mãi mới]()
- Gia dụng giảm sốc đến 50%
- Di động giảm sốc đến 50%
- Trả góp 0% & Khuyến mãi
- Kinh nghiệm mua sắm
- Mẹo vặt đời sống
- Kiến thức
Công thức tính xác suất dễ hiểu và bài tập áp dụng
Tác giả: Ái PhiNgày cập nhật: 04/08/2025 10:36:53Tác giả: Ái Phi14891Bạn có bao giờ tự hỏi xác suất trúng số là bao nhiêu hay khả năng trời mưa chiều nay là thế nào không? Xác suất là một khái niệm quen thuộc, xuất hiện trong cuộc sống hàng ngày từ những trò chơi đơn giản đến các quyết định kinh doanh phức tạp. Trong toán học, xác suất giúp chúng ta đo lường khả năng xảy ra của một sự kiện. Vậy công thức tính xác suất là gì?
Bài viết này sẽ cung cấp cho bạn kiến thức nền tảng về xác suất, các công thức tính xác suất phổ biến kèm theo ví dụ minh họa và bài tập vận dụng cụ thể. Hãy cùng khám phá nhé!
![]()
Công thức tính xác suất
1. Xác suất là gì?
Xác suất là thước đo khả năng một sự kiện xảy ra, thường được biểu diễn bằng một con số từ 0 (không thể xảy ra) đến 1 (chắc chắn xảy ra):
- Xác suất = 0: Biến cố chắc chắn không xảy ra
- Xác suất = 1: Biến cố chắc chắn xảy ra
- Xác suất từ 0 đến 1: Biến cố có khả năng xảy ra ở mức độ tương ứng
Ví dụ: Khi tung một đồng xu, xác suất xuất hiện mặt hình hay mặt số đều là 0.5 vì chỉ có 2 khả năng xảy ra và đều có cơ hội như nhau.

Xác suất là một đại lượng thể hiện mức độ chắc chắn của một biến cố có thể xảy ra
2. Các khái niệm cơ bản trước khi học công thức xác suất
Để sử dụng công thức tính xác suất hiệu quả, bạn cần nắm một số thuật ngữ cơ bản như sau:
- Biến cố (A): Một sự kiện có thể xảy ra hoặc không xảy ra, ví dụ “ra mặt chẵn khi tung xúc xắc”.
- Không gian mẫu (S): Tập hợp tất cả các kết quả có thể xảy ra, ví dụ khi tung một xúc xắc (có 6 mặt) thì S = {1, 2, 3, 4, 5, 6}.
- Biến cố đơn: Chỉ có một kết quả cụ thể.
- Biến cố hợp: Tổng hợp từ hai hay nhiều biến cố.
- Biến cố đối (▁A ): Biến cố không xảy ra nếu A xảy ra và ngược lại.
3. Công thức tính xác suất cơ bản
Dưới đây là các công thức quan trọng bạn cần ghi nhớ:
3.1 Công thức xác suất cổ điển
P(A) = (n(A))/(n(S))
Trong đó:
- P(A): Xác suất xảy ra biến cố A
- n(A): Số trường hợp thuận lợi để A xảy ra
- n(S): Tổng số khả năng có thể xảy ra
Ví dụ: Rút 1 lá bài từ bộ 52 lá, xác suất rút được lá át là: P(A) = 4/52 = 1/13

Xác suất rút được lá át trong bộ bài
3.2 Công thức xác suất có điều kiện
P(A|B)= (P(A∩B))/(P(B))
Ý nghĩa: Xác suất A xảy ra khi biết rằng B đã xảy ra.
Ví dụ: Rút 2 lá bài bất kỳ không hoàn lại. Xác suất cả hai lá đều là quân đỏ sẽ là:
- P (lá đầu tiên là đỏ) = 26/52
- P (lá thứ hai là đỏ | lá đầu tiên đã đỏ) = 25/51
- Xác suất P(A∩B)= 26/52⋅25/51
3.3 Xác suất của biến cố đối
P(▁A) = 1 − P(A)
Ví dụ: Xác suất không rút được quân át từ bộ bài là:
P (▁A) = 1 - 4/52 = 48/52

Xác suất không rút được quân át từ bộ bài
3.4 Công thức cộng xác suất
P(A∪B) = P(A) + P(B) − P(A∩B)
Dùng để tính xác suất khi A hoặc B xảy ra.
3.5 Công thức nhân xác suất
Nếu A và B độc lập:
P(A∩B) = P(A) . P(B)
Nếu A và B không độc lập:
P(A∩B) = P(A) . P(B|A)
4. Một số lưu ý khi áp dụng công thức tính xác suất
Để chắc chắn đáp án trong bài toán tinh xác suất là đúng thì chúng ta cần lưu ý một số vấn đề như sau:
- Luôn xác định đúng không gian mẫu (S) và trường hợp thuận lợi (A)
- Xác định mối quan hệ giữa các biến cố: độc lập, đối lập, giao nhau hay hợp nhau
- Cẩn thận với các tình huống có hoàn lại và không hoàn lại
- Xác suất hợp lệ luôn nằm trong khoảng từ 0 đến 1
5. Bài tập áp dụng công thức tính xác suất
Dưới đây là một số bài tập vận dụng để bạn luyện tập với các công thức tính xác suất bên trên (có đáp án bên dưới):
Bài 1
Tung một đồng xu 3 lần. Tính xác suất để có đúng 2 lần xuất hiện mặt ngửa.
Gợi ý:
Không gian mẫu có 23 = 8 khả năng
Các trường hợp thỏa mãn: (N-N-S), (N-S-N), (S-N-N) → Có 3 trường hợp
Bài 2
Rút 1 lá bài từ bộ bài 52 lá. Tính xác suất để lá bài đó là:
- a. Một quân cơ
- b. Một quân hình bất kỳ (rô, cơ, chuồn, bích)
Bài 3
Một hộp có 5 viên bi đỏ, 4 viên bi xanh, 3 viên bi vàng. Rút ngẫu nhiên 1 viên. Tính xác suất viên bi đó là:
- a. Màu đỏ
- b. Không phải màu đỏ
Đáp án
Bài 1: P = 3/8
Bài 2:
- a. Có 13 quân cơ ⇒ P = 13/52 = 1/4
- b. Tất cả đều là hình ⇒ P = 1
Bài 3: Ta có tổng số viên bi là 12 viên.
- a. P = 5/12
- b. P = 1 - 5/12 = 7/12
6. Kết luận
Hiểu rõ các công thức tính xác suất là nền tảng vững chắc để giải quyết các bài toán xác suất trong học tập và áp dụng hiệu quả vào đời sống. Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về xác suất và vận dụng đúng công thức, nâng cao kỹ năng giải bài.
Oppo Reno13 F (8GB+256GB)
- Reno13F (8+256GB)
- Reno13F 5G (12+256GB)
- Reno13 F 5G (8+256GB)
Vivo V30E (12GB+256GB)
- 12GB+256GB
- 8GB+256GB
Vivo Y100 (8GB+128GB)
- 8GB+128GB
- 8GB+256GB
Apple iPhone 15 128GB
- 128GB
- 256GB
- 512GB
- 15 Plus 128GB
Oppo Find N3 Flip 5G (12GB+256GB)
- Find N3 Flip
- Flip N3 Fold
Samsung Galaxy S25 Ultra 5G (12GB+256GB)
- 12GB+256GB
- 12GB+512GB
- 12GB+1TB
Bài viết liên quan

Số nguyên là gì? Tìm hiểu về số nguyên dương và số nguyên âm
3,026
Công thức tính chu vi hình bình hành kèm ví dụ minh họa dễ hiểu
699
Tổng hợp công thức lượng giác đầy đủ: Tham khảo ngay!
2,393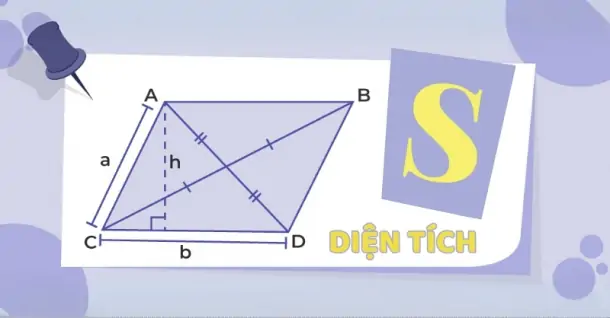
Công thức tính diện tích hình bình hành và bài tập vận dụng
801
Tổng hợp mã bưu chính của tất cả bưu cục tại TP. HCM
2,104
Tra cứu biển số xe 63 tỉnh thành mới và chính xác nhất
1,675Từ khóa
Tải app Dienmaycholon
Tải app theo dõi thông tin đơn hàng và hàng ngàn voucher giảm giá dành cho bạn.

Tin nổi bật

Tết Nhất Có Ai, Mã Đáo Trọn Lộc Tài
Khi mua các dòng TV LG thuộc danh sách khuyến mãi, khách hàng sẽ được tặng quà giá trị tương ứng, bao gồm: - TV LG OLED EVO AI 55C5 – Trị giá 42.090.000đ - TV LG UHD AI 43UA8450 – Trị giá 10...1677
Toshiba Sắm Lớn Cỡ Nào - Lì Xì Cỡ Đó
Khách hàng mua sắm sản phẩm tủ lạnh, máy giặt, máy sấy theo danh sách áp dụng tại hệ thống Siêu Thị Điện Máy - Nội Thất Chợ Lớn trong thời gian diễn ra chương trình sẽ có cơ hội nhận quà tặng hấp dẫn ...4461
Thương hiệu xứng tầm, ưu đãi đẳng cấp - Mua Hisense trúng xe BYD
THƯƠNG HIỆU XỨNG TẦM, ƯU ĐÃI ĐẲNG CẤP ...7054
Tặng Thêm 2 Năm Bảo Hành Và 1 Đổi 1 Trong Vòng 90 Ngày
Khách hàng khi mua máy giặt Toshiba tại hệ thống Siêu thị Điện Máy - Nội Thất Chợ Lớn trên toàn quốc (bao gồm online) trong thời gian diễn ra chương trình sẽ được tận hưởng các ưu đãi sau: - Tặn...1721
Kích Hoạt Chất Đức - Trúng Xe Đức
- Sản phẩm áp dụng: Bếp Đơn, Bếp Đôi, Bếp Ba, Hút Mùi, Lò Vi Sóng, Máy rửa bát thương hiệu JUNGER (chi tiết trong danh sách bên dưới) khi mua sắm tại Siêu Thị Điện Máy - Nội Thất Chợ Lớn. - Hìn...12408
























